Searching For Jeffrey Csima: Parimutuel Pick’em Pools

I’m not afraid of losing a bet…just my readers’ love. Also: PUMP SNEAKERS!

The 1993 film “Searching For Bobby Fischer” is about, according to Wikipedia, parents who “hire a strict instructor who aims to teach the boy to be as aggressive as chess legend Bobby Fischer. The title of the film is a metaphor about the character’s quest to adopt the ideal of Fischer and his determination to win at all costs.” This is a perfect analogy for what we’re going to be discussing today.

Instead of chess, the game in question is the parimutuel NFL pick’em pool. My analysis focuses on the pool offered by the Ontario Lottery Corporation, but the conclusions are likely applicable to other similar games as well. The Ontario Lottery pool works like this:

• You pick every game on the “card”, which usually includes all Sunday + Monday games in a given week.
• Picks are straight up to win, no point spread. If a game ends in a tie, the visiting team gets credited with the win.
• Tickets cost $5, with the option to play multiple combinations by “boxing” 1/2/3/4 games at a cost of $10/$20/$40/$80.
• Money from ticket purchases is pooled together, with 40% raked off the top and the other 60% split among the winning tickets.
• If nobody has a perfect card, the winnings are split among the cards with 1 wrong selection.

This game is fairly popular in Ontario, with an average of around 200,000 tickets played each week for a total pool of around $1 million and a prize pool of around $600,000. Like horse racing, this type of bet belongs to a class called “parimutuel” because you are playing against other players, while the “house” takes a fixed cut and has no stake in who wins or loses.

Playing the part of Bobby Fischer, our role model is Jeffrey Csima. I have never met Mr. Csima, and I have no idea whether he’ll be flattered or annoyed that I’m writing about him…given the nature of what we’re talking about, I’m guessing the latter. Even though we’ve never met, I’ve read a lot about him. Because this pool is run by the provincial lottery corporation, big winners get the jackpot treatment, big novelty cheque and all…and this guy has received quite a few of them. His frequency of big wins can be explained by neither luck nor skill alone, it’s almost certain that he is flooding the pools with many combinations each week. But why? Has he “solved” the game and found +EV? I believe he has.

I, of course, will be your strict instructor. Now drop and give me 20, and let’s begin.

First let’s address the monster in the room, that 40% takeout. Yes, it’s high. Yes, it sucks. But there are good reasons to believe that it can be overcome:

• The parimutuel nature of this. I like our chances of beating the public by enough to overcome the 40% vig way more than I would like our chances of beating a bookmaker by that kind of margin.
• The high variance. Beating the vig is much easier, relatively speaking, on a huge longshot parlay (which is essentially what this is) than on a single even money bet. Plus, if you were to parlay 15 legs together at -110 odds, you’d be paying a compounded vig of 50% so you’re comparatively better off this way!

The truth is, this game is something I’ve been thinking about for many years and one that many people have asked me about. The win probability of any given ticket can easily be calculated from the money line odds of each game. It’s the payout that’s the tough part because it requires estimation of the distribution of all tickets in the pool and 1 pool a week is not a lot of data to work with. That answer didn’t satisfy Twitter follower Underdobs, who promptly filed a Freedom of Information request to get data for pools going back to 2004. Excluding the occasional pool where there was no perfect card and those that I couldn’t match up to my historical database left me with 242 pools worth of data…enough to get me sufficiently interested to at least try an analysis!

Let’s define the “theoretical value” of a pools ticket by taking its component money lines, removing the vig and parlaying them together. So a $5 ticket that’s equivalent to a money line parlay with no-vig odds of 10,000 for 1 would be assigned a theoretical value of $50,000. For tickets that won in the past, we can use that theoretical value as a basis of comparison to the actual payout that the winners received. If that same ticket with $50,000 theoretical value won and paid $40,000, the relative difference of -20% is a good (retrospective) measure of what the ticket’s EV was.

Of course, an EV measure that only works retrospectively isn’t much use to us. We need to find factors that are known before the games start and are predictive of the ratio of actual payout to theoretical EV.

Let’s start with a little exploratory data analysis…

The average payout among the 242 winners was 1.28 x theoretical value; a number that, while skewed, at least gives some hope that this game can be beaten. 103 out of 242 winners (43% of winners) paid out more than 1.00 x theoretical.

The smallest payout in my data set occurred in 2006 week 5. The Colts, as -2000 favourites, needed a 4th quarter comeback to beat the Titans. Favourites went 13-1 straight up that week, with the one winning dog (using that term very loosely) the Eagles who overcame -102/-108 odds to beat the Cowboys. There were 5,297 very disappointed people who woke up on Tuesday morning to discover that their perfect 14-0 pools card paid out the paltry sum of $83.30. The theoretical value of that chalky ticket was $770, for an EV of -89%. Ouch.

The largest payout in my data set occurred in 2011 week 15. The week featured several upsets including Kansas City +475/-569 over Green Bay, Washington +235/-265 over the Giants and Indianapolis +252/-285 over Tennessee. Of the 291,619 tickets played that week, a single one went 14-0 and scooped the entire prize pool of $874,857. The theoretical value of that ticket was $230,552 for an EV of +279%.

So we already have some clues as to what makes a +EV ticket. It makes sense that the ease of access and the $5 price make these pools attractive to the kinds of casual fans and unsophisticated bettors who look at them as a simple prediction contest rather than with any notion of “value”. Therefore, favourites are overrepresented and underdogs are underrepresented in the distribution of the public’s picks, and there will be an inverse relationship between win probability and EV. Does this hypothesis hold up across all 242 pools?

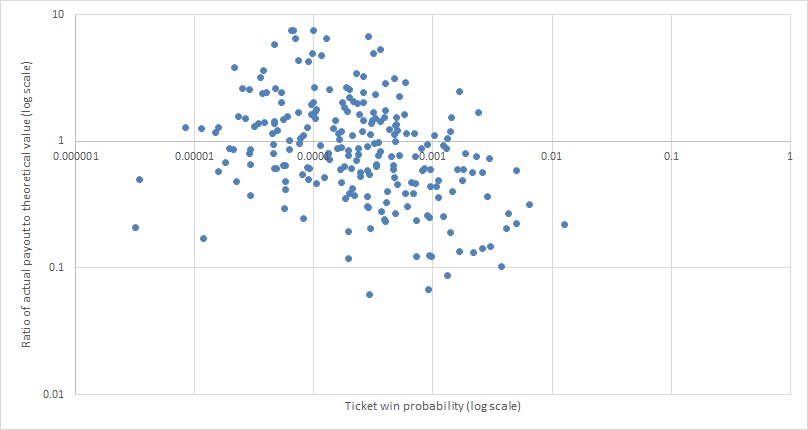
It sure does! Well….with a couple of exceptions. See those two points at the far left, with win probability between 0.000001 and 0.00001 and -EV? Those are tickets with such high theoretical value that it would take a payout in excess of the entire prize pool to make them +EV. For example, if the prize pool is $700,000 and you pick a ticket with a theoretical value of $2,000,000, even if you could somehow guarantee that you are the only person with that ticket your maximum possible payout would be $700,000. So you want a dog-heavy ticket, but don’t go too overboard with it!

Like in any parimutuel product, the way to find value is by identifying and exploiting errors that your fellow players are making. The favourite bias described above is by far the most significant one – you could randomly make a ticket and as long as it has between 0.0001 and 0.00001 win probability (equivalent to theoretical value between $50,000 and $500,000) your ticket is more likely than not to be +EV. If you don’t want to bother converting the money lines to vig-free numbers to calculate the theoretical value, you can calculate the payout on a regular money line parlay – anything in the range from $25,000 to $250,000 would be your +EV sweet spot on that basis. Maybe a little lower than that if it’s a big bye week and there are only 12 or 13 games on the card, but not much.

Of course, with these types of extreme longshots the EV matters much less than the variance. A $5 bet with 1 in 10,000 odds of winning is not something professional gamblers find attractive. My advice? Look at these like lottery tickets. People don’t buy lottery tickets because they’re +EV, they buy them for the thrill of the possibility of a huge win. If you can get that thrill in a +EV situation, all the better! Set aside $5 or $10 or $20 or $40 or $80 each week of money that you can afford and you have every expectation of losing, and shoot your shot. That’s what I’ll be doing. If you play the lottery each week, switch to this instead!

We’ve covered the biggest finding already, but there are some other small things you can add to your strategy to squeeze out a little more EV:

Pick more home teams. The public tends to weigh the probability of team A beating team B using the relative strength of each team, without accounting for home field advantage. Tickets with more home teams tend to pay a little more than tickets with fewer home teams.

Pick primetime favourites. There’s nothing worse than going into Sunday Night Football / Monday Night Football with a perfect card and losing it on one of the last two games. To avoid this psychological unpleasantness, people like to box the primetime games so they can lock in a winner. I don’t have enough data to prove this conclusively, but I believe that this would make the underdogs overplayed in prime time games.

Fade the public. Going along with the theory that our fellow competitors are unsophisticated, they will likely overpick teams that are well known and have a lot of fans, the so-called “public” teams. This is another one that’s tough to prove because the data spans 16 years and public perception of teams changes over time…except for one. Ladies and gentlemen, the New England Patriots.

Box carefully. From speaking with people in the know about these things, apparently a common strategy among sharp syndicates is to box the largest underdogs…which is not a bad strategy, but it’s not how I’d recommend to play it. Suppose you box the 4 largest dogs and play favourites on the rest of the card – that’s 16 tickets for $80. One of those tickets will have all favourites, which puts you squarely in $83 payout, -89% EV hell. One of them will have all dogs, which probably puts you outside of the +EV sweet spot on the other side. Your 16 tickets will have too wide of a range in their theoretical value. Instead I would start with a ticket that is in the sweet spot, and then widen that ticket by boxing the games that are the closest to 50-50, which ensures that your theoretical values will be tightly clustered within that sweet spot.

Again, these things are only marginally helpful compared to the main finding here. Just like Bobby Fischer (and presumably like Jeffrey Csima), we win by being aggressive. If you have a perfect card and your ticket pays less than $20,000, you’re doing it wrong (or perhaps you’re doing it right and WAY too many people have read this article. Another thing about parimutuel systems is that +EV bets become -EV when they get too crowded…)

Good luck, and tag me on twitter with photos of your big novelty cheques! If you see Mr. Csima at the prize office, please tell him I’m a big fan.